

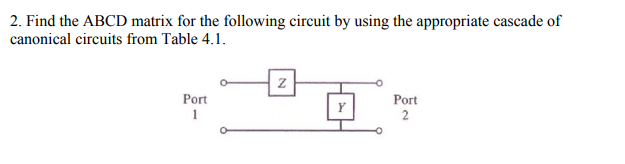
Recall that the wavefront curvature R(z) and the radius $\omega(z)$ are not independent but are connected by the q-parameter as: An ABCD matrix 1 is a 2-by-2 matrix associated with an optical element which can be used for describing the elements effect on a laser beam. We can therefore use this formulation to describe how the wavefront radius can be modified by optical elements. We know from paraxial geometrical optics that the effect of the optical elements on the wavefront radius can be described by the ABCD law of ray transfer matrices. This relation helps in determining the fourth parameters if we know any three parameters.įor a symmetrical network, the input and output terminal may be interchanged without affecting the network behaviour.Because of the paraxial/Fresnel approximation, a Gaussian beam maintains its profile as it propagates in space, with the only parameter parameter changing being its wavefront radius R(z). ABCD Matrices The ABCD matrix is a simple way of representing paraxial optical components, i.e. Then whole optical systems are reduced to a single matrix by multiplying. examples of how the equations can be used. So the current remains same I s = I r.ĭividing the above equation from -V/B we get, Represent each interface or transition by an appropriate ABCD, or transfer matrix. it contains only passive components in the circuit like inductance, resistance, etc. The current flows through the receiving end is given by the equationĬonsider, the network is passive, i.e. Thus, the direction of the current in the network changes, which is shown in the diagram below

param d Structure containing frequency and network arrays: d.freq frequency array (with properties min, max, log) d.abcd abcd matrix array d.src source impedance array d.src.eq source equivalent type (0 Thevenin, 1 Norton) d.load load impedance array d.load.

Similarly, the voltage is applied at the receiving end, and the input voltage remains zero. Functions for converting the filterData structure into analytical measurements. Since, under short circuit the receiving end voltage is zero, the voltage and current equations become The colors here can help determine first, whether two matrices can be multiplied, and second, the dimensions of the resulting matrix. The voltage V is applied to the sending end, and the receiving end is kept short circuit, so the voltage becomes zero. When multiplying two matrices, the resulting matrix will have the same number of rows as the first matrix, in this case A, and the same number of columns as the second matrix, B.Since A is 2 × 3 and B is 3 × 4, C will be a 2 × 4 matrix. Relation between ABCD parametersįor determining the relation between various types of network, like passive or bilateral network reciprocity theorem is applied. We get the value of D, which is the ratio of the sending current to the receiving current. However chaining them is easier (as a computation) so thats why they are used. They carry the same information as the S parameter, which are important since they are easy to measure (for some definition of ease). An elements effect on a ray is found by multiplying its ray vector. Similarly, if we put V r= 0 in current equations, As far as I know they are simply a mathematical artifact to help in calculation. Thus, we can define 2 x 2 ray matrices for any element. If we put V r = 0 in the equation, we get the value of B which is the ratio of sending end voltage to the receiving end currents. However, any of these three methods will produce the same result. The inverse of a matrix can be found using the three different methods. Finding the inverse of a 3×3 matrix is a bit more difficult than finding the inverses of a 2 ×2 matrix. ABCD parameters for short circuitįor the short circuit, the voltage remains zero at the receiving end. The inverse matrix can be found for 2× 2, 3× 3, n × n matrices. We get the value of c parameter which is the ratio of the sending end voltage to the current. Similarly, if I r =0 is substituted in current equation, It is a dimensionless constant because their ratio has the same dimension. Since the circuit is open at the receiving end, the current I r remains zero.įrom above equations, we get the value of A parameter which is the ratio of sending end voltage to the receiving end voltage. In the open circuit, the output terminals are open, and the voltage measure across them is V r.


 0 kommentar(er)
0 kommentar(er)
